アインシュタインが「複利は人類最大の発明である」という言葉を残したのはご存じだろうか。私もこの言葉を知ったのはここ1,2年のことである。今回はこの複利とはどういうものかと複利のすごさについて解説していく。
複利・単利の違いについて
「複利」とは利子にもさらに利子がつくことである。ちなみに,対義語として「単利」というものもある。単利は元金にしか利子がつかないことである。
複利と単利の違いの例
例をあげて説明すると次のようなことである。年利10%の場合であり,ともに元金100万円である。表は単位を省略してある。
| 元金 | 1年目終わり | 2年目終わり | 3年目終わり | ・・・ | 10年目終わり | |
| 複利 | 100 | 110 | 121 | 133.1 | ・・・ | 約259.37 |
| 100×10%=10増 | 110×10%=11増 | 121×10%=12.1増 | 23.58増 | |||
| 単利 | 100 | 110 | 120 | 130 | ・・・ | 200 |
| 100×10%=10増 | 100×10%=10増 | 100×10%=10増 | 100×10%=10増 |
上の例から分かるように,複利には利子に利子がつくので増加する額(利子)が毎年増えるのに対して,単利は元金が100なので毎年増える額(利子)は一定の10なのである。10年目終わりにそれぞれが保有している資産の差が$259.37-200=59.37$なので,元金が一緒でも59.37万円の差が出る。これは大きいと感じるのではないか。この例は利子に利子がつくとここまで大きな差が出る一つであるが,さらに複利の破壊力を感じるものがあるので次の例を考えてほしい。
複利の破壊力
AさんとBさんは同級生で二人は高校を卒業後,Aさんは就職し,Bさんは大学へ進学した。そして,Aさんは20歳のときに100万円を投資した。Bさんは30歳のときに200万円を投資した。AさんとBさんともに同じ投資商品(年利10%,複利)である。この二人が60歳のときの資産はどちらが多いか。
さて,この問題を解くためには次のことが分かっている必要がる。それはn年後にその資産が元金の何倍になるかの計算式である。では,1年後には資産が何倍になるのか。それは10%の場合$1+0.1=1.1$倍である。そして,2年後はというと$1.1^{2}$倍である。そう,n年後は$1.1^{n}$になるのだ。ということで,Aさんの資産の計算式は$$100×1.1^{40}万円$$である。そしてBさんの資産は$$200×1.1^{30}万円$$である。
指数関数の利用
ここで,$1.1^{40}$や$1.1^{30}$の計算についてだが,もちろん手計算では不可能に近い。少なくとも私は手計算せずパソコンで求める。しかし,いざパソコン・スマホが使用不可の試験でもし近似値をもとめなければならなくなったらどうするか。一般には常用対数表を用いるやり方である。その方法はまた後日,記事にしようと思う。(後日の記事「常用対数表を用いて累乗を計算しよう!」)今回は計算された値を用いる。$$1.1^{40}\fallingdotseq45.259$$$$1.1^{30}\fallingdotseq17.449$$であるので,AさんとBさんの資産はそれぞれ次のとおりである。$$Aさん\hspace{20pt} 100×45.259=4525.9万円$$ $$Bさん\hspace{20pt} 200×17.449=3489.8万円$$結論はAさんの方が約1036万円多いのである。この差を読者はどう感じるであろうか。私はここまで違うのかと驚いた。てっきりBさんの投資額が多いのだから,Bさんの方が多いではと思っていたからである。しかし,計算結果はAさんが多い。しかも1000万円もの大差である。ここで「あと10年経てば,いやもう少し立てばBさんが逆転する」と考えた人もいるかもしれない。しかし,実はこれは何年経とうともBさんがAさんを上回ることはできないのである。それは,指数関数を学んでいれば分かると思う。下のグラフはAさんとBさんの資産の額を表したものである。
指数関数を用いた資産のグラフ
横軸が二人の年齢,縦軸が資産額(単位は万円)。緑がAさん,赤がBさんの資産額の関数。geogebra使用
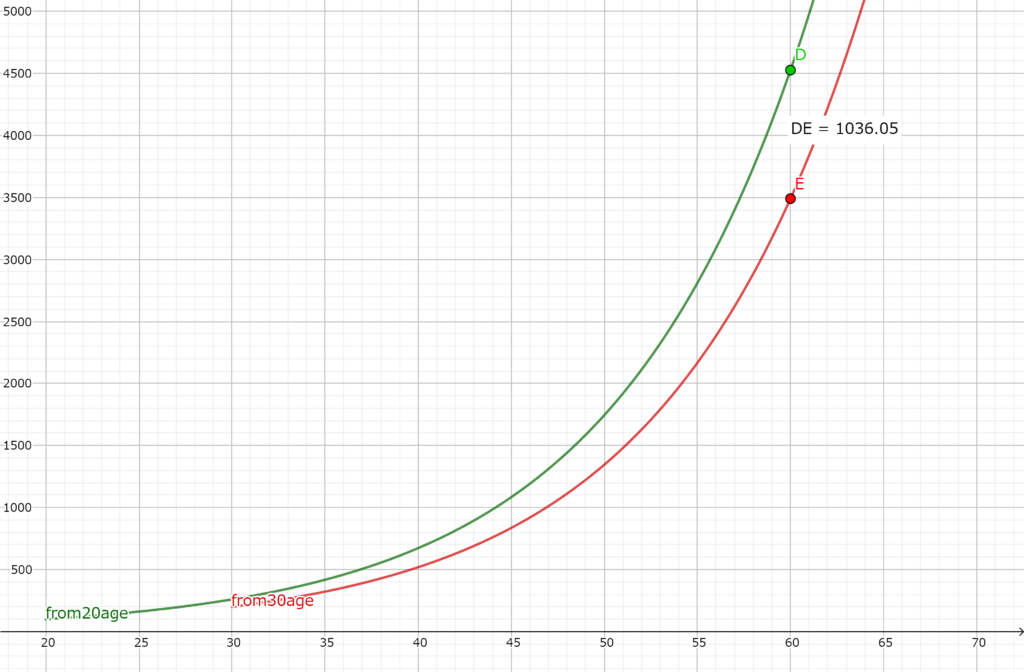
年数が経てば経つほど二人の差が広がっていくのが分かる。ちなみに,Aさんのグラフに式は$$y=100・1.1^{x-20}$$である。Bさんのグラフの式は$$y=200・1.1^{x-30}$$である。
指数関数から分かること
このグラフを見れば分かると思うが,年齢が高くなるにつれて上がり幅大きくなる。例えばAさんの20歳から30歳までの資産の増えた差分は$259.3-100=159.3万円$であるのに対し,50歳から60歳までの資産に増えた差分は$4525.9-1744.9=2781万円$である。同じ10年間でも,経てば経つほど増加スピード大きくなるのが指数関数の特徴である。ちなみに,2次関数も増加スピードが大きくなるが指数関数の比ではない。つまり,期間が長くなれば長くなるほど増える額も大きくなる。ちなみに,Aさんの70歳時点での資産保有額は$1.1^{50}\fallingdotseq117.391$であることを用いると,$$100\times117.391=11739.1万円$$20歳の時の100万の投資が70歳の時に億を超えて1億1739万円にもなってしまう。60歳から70歳にかけて資産を7215万も増やしているのだ。これが複利の一番の破壊力である。
まとめ
このことから,時間をかけると複利の力が爆発的に伸びるということが分かる。資産形成も若いうちから考えておくというのは重要なのかもしれない。今回の学びは「複利の計算は指数関数を用いて考えることができるということ」である。自分の資産形成を考えるとき,この複利の計算では指数関数の考えを用いて自分で求めることができるようになってほしい。



コメント