72の法則はご存じですか?最近、投資に関するYoutubeなどのSNSで頻繁に耳にする言葉です。
今回は72の法則ってどうやって導かれたのかを数学的に紹介していこうと思います。
72の法則
72の法則
投資等において72を年間利回り(%)で割ると元金が2倍になる年数がおおよそ計算できる
例をあげると年間利回り4%で運用すると2倍になるのに
$$72÷4 (%)=18 年$$
おおよそ18年かかるということである。
ではなぜ72で利回りを割ると2倍になる年数が分かるのか,今回はそれを数学的に求めてみよう。
ここで使われる数学の知識は指数・対数・微分の定義である。より正確なことを知りたければテイラー展開が必要であるが今回は、高校生でも理解できるように構成したあります。
72の法則の証明
年利を$100x$%,元手が2倍になるまでの年数を$n$とする.すると次の式が導かれる.
$$(1+x)^{n}=2$$
等式の左辺は年利$100x$%で$n$年運用した場合の元金からの倍率になっている.そしてこの式を$n$について解いていけばよい.
この等式の両辺に自然対数をとって求めていく.
$$\begin{split}
\log(1+x)^{n}&=\log{2}より\\
n\log(1+x)&=\log{2}\\
\end{split}$$
そして両辺を$\log(1+x)$で割ると
$$n=\frac{\log{2}}{\log(1+x)}$$
となる.分子の$\log{2}$の値は調べられていて,$\log{2}\fallingdotseq0.693146・・・$である.
あとは分母の$x$に利回りの値を代入れば良い.しかし$2$%の値を代入したところで$\log1.02$の値なんてわからないし,そもそも72で割るのとは?という疑問が残る.
ここからの解説を扱っているサイトは少ないのでは私は思っています.
なのでここからは必見です.
これを問題を解消するのに微分の定義を使う.
微分の定義
$x=a$における微分係数
$$f'(a)=\lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}$$
これは$x$を$a$に限りなく近づけていくと等式が成り立つことを示してる.今回$a=0$として考える.なので利回りを2%や5%程度であれば実際の$x$の値は0.02や0.05なので0に近い値といっても良いしたがって,上の式は$x$が$0$に近い値であれば次のように見ることができる.
$$\begin{split}
f'(0)&\fallingdotseq \frac{f(x)-f(0)}{x}より\\
\\
f(x)&\fallingdotseq f(0)+f'(0)x ・・・①
\end{split}$$
ここで$f(x)=\log(1+x)$とおけば,$f'(x)=$$\frac{1}{1+x}$なので$f'(0)=1$となる.
よって①から
$$\log(1+x)\fallingdotseq x$$
したがって,
$n=$$\frac{\log2}{x}$なので利回りで$\log2$を割れば年数がでる.分母分子に100を掛ければ
$$n=\frac{69.3146}{100x}\hspace{10px}(分母は%)$$
つまり,約69を%で割るのだがここで「69?なの。72ではないじゃん」とツッコミが入りそうではあるが実際は72の法則ではなく69の法則なのである.
なぜ72の法則になったのか
その理由は約数に関係している。$69$の約数は$69$を素因数分解すると簡単に求めることができる。
$$69=3・23$$より$1と3と23と69$である。
つまり,利回りが1%と3%(23%や69%は値として大きいので除外)であれば69を割った時に整数になるので考えやすい。しかし,それ以外の利回りでは整数にならずに小数になってしまうので考えにくくなってしまうのである。なので,69に近い整数で約数の種類が多いものは何かないかなと探してみたいと思う。
そこで69に近い整数の約数を挙げていくと次のようになる。
64 → 1,2,4,8,16,32,64
65 → 1,5,13,65
66 → 1,2,3,6,11,22,33,66
67 → 1,67
68 → 1,2,4,17,34,68
69 → 1,3,23,69
70 → 1,2,5,7,10,14,35,70
71 → 1,71
72 → 1,2,3,4,6,8,9,12,18,24,36,72
73 → 1,73
74 → 1,2,37,74
この中で約数が多いのが72なのだ。
しかも,72が良い理由がもう一つある。それは,$\log(x+1)\fallingdotseq x$と置き換える際,この式は近似なので真の値と少しズレてしまう。
どれくらいズレてしまうのかの例を挙げると次のとおりである。
$$\begin{split}
\log(1+0.01)&=0.00432137378<0.01\\
\log(1+0.02)&=0.00860017176<0.02\\
\log(1+0.03)&=0.01283722470<0.03\\
\log(1+0.04)&=0.01703333929<0.04\\
\log(1+0.05)&=0.02118929906<0.05\\
\log(1+0.06)&=0.02530586526<0.06\\
\end{split}$$
どれを見ても,真の値である$\log(x+1)$より$x$の方が少し大きいのだ。なので分母を$x$をしたつまり,大きくしたのであれば分子もそれにしたがって69より少し大きい方がのぞましい。
そんな理由もあり72を使われるようになったのである。
$\log(1+x)$を$x$とした場合,そのままの場合どれくらい真の値とズレるのか
$x$が0に近い値の場合は$\log(1+x)\fallingdotseq x$として良いといったがあまり納得できない読者はいるのではと思うので,実際に上のような近似をした場合としない場合でどれだけズレが生じるのかをグラフにしてみたので見てみよう。
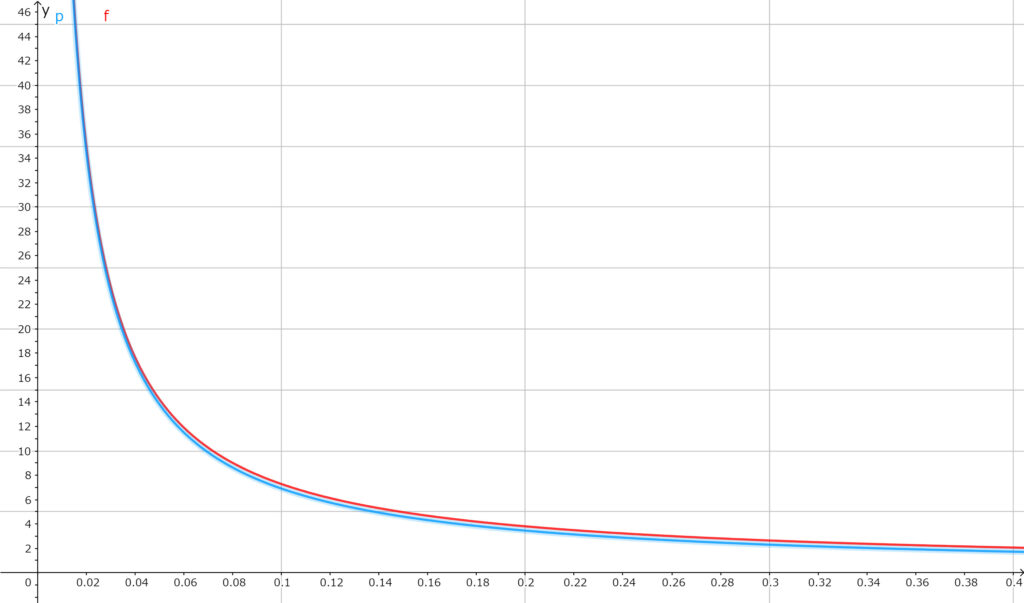
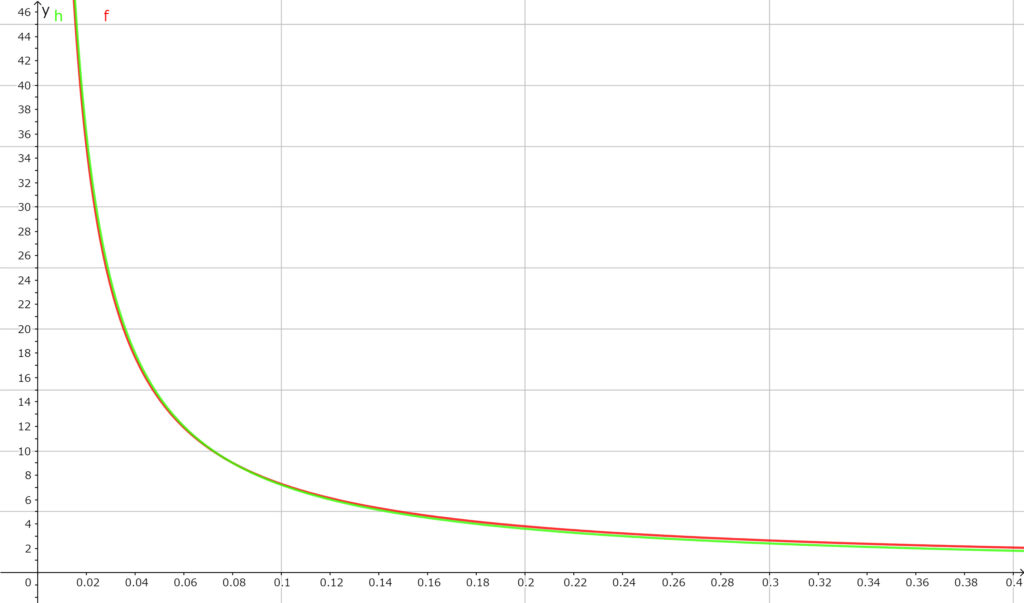
2つのグラフに共通していることとして赤いグラフは真のグラフである。つまり
$$n=\frac{\log2}{\log(1+x)}$$
である。
上側の青色のグラフが69の法則。つまり分子を69のままであるので
$$n=\frac{69}{x}$$
の式から作られたグラフである。
下側の緑色のグラフが72の法則。つまり分子を72に変えたもので
$$n=\frac{72}{x}$$
の式から作られたグラフである。
これら2つのグラフから気が付くこと
$\log(1+x)\fallingdotseq x$と変換しても$x$が0に近い値では真のグラフから大きくハズれることもないことが視覚的にも分かったのではと思う。
また、69のままでも72に変えても真のグラフと大して差がないことが視覚的にも分かったのではと思う。
しかも$x$が0から離れた値の場合、72の法則のグラフの方が69の法則グラフのよりも真のグラフに近いというのも見えてくる。
まとめ
今まで72の法則の結論のみを覚えている方は実はその法則を導く裏では数学の微分が使われていることを知っていてもらえると数学者の苦労も報われるのでは思う今日この頃。
日常には数学に満ち溢れている。数学なんて四則演算ができれば十分だなんて言われることもあるが、やっぱり法則の原点が見えると世界がもっと面白く見えるのではないでしょうか?




コメント